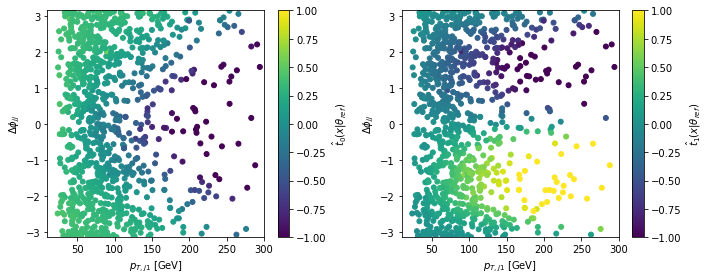MadMiner physics tutorial (part 3B)#
Johann Brehmer, Felix Kling, Irina Espejo, and Kyle Cranmer 2018-2019
In part 3A of this tutorial we will finally train a neural network to estimate likelihood ratios. We assume that you have run part 1 and 2A of this tutorial. If, instead of 2A, you have run part 2B, you just have to load a different filename later.
Preparations#
Make sure you’ve run the first tutorial before executing this notebook!
import logging
import numpy as np
import matplotlib
from matplotlib import pyplot as plt
%matplotlib inline
from madminer.sampling import SampleAugmenter
from madminer import sampling
from madminer.ml import ScoreEstimator
# MadMiner output
logging.basicConfig(
format='%(asctime)-5.5s %(name)-20.20s %(levelname)-7.7s %(message)s',
datefmt='%H:%M',
level=logging.INFO
)
# Output of all other modules (e.g. matplotlib)
for key in logging.Logger.manager.loggerDict:
if "madminer" not in key:
logging.getLogger(key).setLevel(logging.WARNING)
1. Make (unweighted) training and test samples with augmented data#
At this point, we have all the information we need from the simulations. But the data is not quite ready to be used for machine learning. The madminer.sampling class SampleAugmenter will take care of the remaining book-keeping steps before we can train our estimators:
First, it unweights the samples, i.e. for a given parameter vector theta (or a distribution p(theta)) it picks events x such that their distribution follows p(x|theta). The selected samples will all come from the event file we have so far, but their frequency is changed – some events will appear multiple times, some will disappear.
Second, SampleAugmenter calculates all the augmented data (“gold”) that is the key to our new inference methods. Depending on the specific technique, these are the joint likelihood ratio and / or the joint score. It saves all these pieces of information for the selected events in a set of numpy files that can easily be used in any machine learning framework.
sampler = SampleAugmenter('data/lhe_data_shuffled.h5')
# sampler = SampleAugmenter('data/delphes_data_shuffled.h5')
19:25 madminer.analysis INFO Loading data from data/lhe_data_shuffled.h5
19:25 madminer.analysis INFO Found 2 parameters
19:25 madminer.analysis INFO Did not find nuisance parameters
19:25 madminer.analysis INFO Found 6 benchmarks, of which 6 physical
19:25 madminer.analysis INFO Found 3 observables
19:25 madminer.analysis INFO Found 89991 events
19:25 madminer.analysis INFO 49991 signal events sampled from benchmark sm
19:25 madminer.analysis INFO 10000 signal events sampled from benchmark w
19:25 madminer.analysis INFO 10000 signal events sampled from benchmark neg_w
19:25 madminer.analysis INFO 10000 signal events sampled from benchmark ww
19:25 madminer.analysis INFO 10000 signal events sampled from benchmark neg_ww
19:25 madminer.analysis INFO Found morphing setup with 6 components
19:25 madminer.analysis INFO Did not find nuisance morphing setup
The relevant SampleAugmenter function for local score estimators is extract_samples_train_local(). As in part 3a of the tutorial, for the argument theta you can use the helper functions sampling.benchmark(), sampling.benchmarks(), sampling.morphing_point(), sampling.morphing_points(), and sampling.random_morphing_points().
x, theta, t_xz, _ = sampler.sample_train_local(
theta=sampling.benchmark('sm'),
n_samples=500000,
folder='./data/samples',
filename='train_score'
)
19:25 madminer.sampling INFO Extracting training sample for local score regression. Sampling and score evaluation according to sm
19:25 madminer.sampling INFO Starting sampling serially
19:25 madminer.sampling INFO Sampling from parameter point 1 / 1
19:25 madminer.sampling INFO Effective number of samples: mean 29966.000000000004, with individual thetas ranging from 29966.000000000004 to 29966.000000000004
We can use the same data as in part 3a, so you only have to execute this if you haven’t gone through tutorial 3a:
_ = sampler.sample_test(
theta=sampling.benchmark('sm'),
n_samples=1000,
folder='./data/samples',
filename='test'
)
19:25 madminer.sampling INFO Extracting evaluation sample. Sampling according to sm
19:25 madminer.sampling INFO Starting sampling serially
19:25 madminer.sampling INFO Sampling from parameter point 1 / 1
19:25 madminer.sampling INFO Effective number of samples: mean 10097.0, with individual thetas ranging from 10097.0 to 10097.0
2. Train score estimator#
It’s now time to build a neural network. Only this time, instead of the likelihood ratio itself, we will estimate the gradient of the log likelihood with respect to the theory parameters – the score. To be precise, the output of the neural network is an estimate of the score at some reference parameter point, for instance the Standard Model. A neural network that estimates this “local” score can be used to calculate the Fisher information at that point. The estimated score can also be used as a machine learning version of Optimal Observables, and likelihoods can be estimated based on density estimation in the estimated score space. This method for likelihood ratio estimation is called SALLY, and there is a closely related version called SALLINO. Both are explained in “Constraining Effective Field Theories With Machine Learning” and “A Guide to Constraining Effective Field Theories With Machine Learning”.
The central object for this is the madminer.ml.ScoreEstimator class:
estimator = ScoreEstimator(n_hidden=(30,30))
estimator.train(
method='sally',
x='data/samples/x_train_score.npy',
t_xz='data/samples/t_xz_train_score.npy',
)
estimator.save('models/sally')
19:25 madminer.ml INFO Starting training
19:25 madminer.ml INFO Batch size: 128
19:25 madminer.ml INFO Optimizer: amsgrad
19:25 madminer.ml INFO Epochs: 50
19:25 madminer.ml INFO Learning rate: 0.001 initially, decaying to 0.0001
19:25 madminer.ml INFO Validation split: 0.25
19:25 madminer.ml INFO Early stopping: True
19:25 madminer.ml INFO Scale inputs: True
19:25 madminer.ml INFO Shuffle labels False
19:25 madminer.ml INFO Samples: all
19:25 madminer.ml INFO Loading training data
19:25 madminer.utils.vario INFO Loading data/samples/x_train_score.npy into RAM
19:25 madminer.utils.vario INFO Loading data/samples/t_xz_train_score.npy into RAM
19:25 madminer.ml INFO Found 500000 samples with 2 parameters and 3 observables
19:25 madminer.ml INFO Setting up input rescaling
19:25 madminer.ml INFO Creating model
19:25 madminer.ml INFO Training model
19:25 madminer.utils.ml.tr INFO Training on CPU with single precision
19:26 madminer.utils.ml.tr INFO Epoch 3: train loss 0.24239 (mse_score: 0.242)
19:26 madminer.utils.ml.tr INFO val. loss 0.25060 (mse_score: 0.251)
19:27 madminer.utils.ml.tr INFO Epoch 6: train loss 0.22593 (mse_score: 0.226)
19:27 madminer.utils.ml.tr INFO val. loss 0.23032 (mse_score: 0.230)
19:28 madminer.utils.ml.tr INFO Epoch 9: train loss 0.21441 (mse_score: 0.214)
19:28 madminer.utils.ml.tr INFO val. loss 0.21741 (mse_score: 0.217)
19:29 madminer.utils.ml.tr INFO Epoch 12: train loss 0.20653 (mse_score: 0.207)
19:29 madminer.utils.ml.tr INFO val. loss 0.20709 (mse_score: 0.207)
19:30 madminer.utils.ml.tr INFO Epoch 15: train loss 0.19986 (mse_score: 0.200)
19:30 madminer.utils.ml.tr INFO val. loss 0.19887 (mse_score: 0.199)
19:31 madminer.utils.ml.tr INFO Epoch 18: train loss 0.19441 (mse_score: 0.194)
19:31 madminer.utils.ml.tr INFO val. loss 0.19143 (mse_score: 0.191)
19:32 madminer.utils.ml.tr INFO Epoch 21: train loss 0.19016 (mse_score: 0.190)
19:32 madminer.utils.ml.tr INFO val. loss 0.18850 (mse_score: 0.189)
19:33 madminer.utils.ml.tr INFO Epoch 24: train loss 0.18647 (mse_score: 0.186)
19:33 madminer.utils.ml.tr INFO val. loss 0.18236 (mse_score: 0.182)
19:35 madminer.utils.ml.tr INFO Epoch 27: train loss 0.18417 (mse_score: 0.184)
19:35 madminer.utils.ml.tr INFO val. loss 0.18023 (mse_score: 0.180)
19:36 madminer.utils.ml.tr INFO Epoch 30: train loss 0.18195 (mse_score: 0.182)
19:36 madminer.utils.ml.tr INFO val. loss 0.17799 (mse_score: 0.178)
19:37 madminer.utils.ml.tr INFO Epoch 33: train loss 0.17990 (mse_score: 0.180)
19:37 madminer.utils.ml.tr INFO val. loss 0.17600 (mse_score: 0.176)
19:38 madminer.utils.ml.tr INFO Epoch 36: train loss 0.17840 (mse_score: 0.178)
19:38 madminer.utils.ml.tr INFO val. loss 0.17421 (mse_score: 0.174)
19:39 madminer.utils.ml.tr INFO Epoch 39: train loss 0.17712 (mse_score: 0.177)
19:39 madminer.utils.ml.tr INFO val. loss 0.17329 (mse_score: 0.173)
19:40 madminer.utils.ml.tr INFO Epoch 42: train loss 0.17623 (mse_score: 0.176)
19:40 madminer.utils.ml.tr INFO val. loss 0.17126 (mse_score: 0.171)
19:41 madminer.utils.ml.tr INFO Epoch 45: train loss 0.17538 (mse_score: 0.175)
19:41 madminer.utils.ml.tr INFO val. loss 0.17093 (mse_score: 0.171)
19:42 madminer.utils.ml.tr INFO Epoch 48: train loss 0.17472 (mse_score: 0.175)
19:42 madminer.utils.ml.tr INFO val. loss 0.17005 (mse_score: 0.170)
19:43 madminer.utils.ml.tr INFO Early stopping after epoch 49, with loss 0.16998 compared to final loss 0.17045
19:43 madminer.utils.ml.tr INFO Training time spend on:
19:43 madminer.utils.ml.tr INFO initialize model: 0.00h
19:43 madminer.utils.ml.tr INFO ALL: 0.31h
19:43 madminer.utils.ml.tr INFO check data: 0.00h
19:43 madminer.utils.ml.tr INFO make dataset: 0.00h
19:43 madminer.utils.ml.tr INFO make dataloader: 0.00h
19:43 madminer.utils.ml.tr INFO setup optimizer: 0.00h
19:43 madminer.utils.ml.tr INFO initialize training: 0.00h
19:43 madminer.utils.ml.tr INFO set lr: 0.00h
19:43 madminer.utils.ml.tr INFO load training batch: 0.10h
19:43 madminer.utils.ml.tr INFO fwd: move data: 0.00h
19:43 madminer.utils.ml.tr INFO fwd: check for nans: 0.03h
19:43 madminer.utils.ml.tr INFO fwd: model.forward: 0.05h
19:43 madminer.utils.ml.tr INFO fwd: calculate losses: 0.01h
19:43 madminer.utils.ml.tr INFO training forward pass: 0.07h
19:43 madminer.utils.ml.tr INFO training sum losses: 0.01h
19:43 madminer.utils.ml.tr INFO opt: zero grad: 0.00h
19:43 madminer.utils.ml.tr INFO opt: backward: 0.04h
19:43 madminer.utils.ml.tr INFO opt: clip grad norm: 0.00h
19:43 madminer.utils.ml.tr INFO opt: step: 0.02h
19:43 madminer.utils.ml.tr INFO optimizer step: 0.06h
19:43 madminer.utils.ml.tr INFO load validation batch: 0.04h
19:43 madminer.utils.ml.tr INFO validation forward pass: 0.02h
19:43 madminer.utils.ml.tr INFO validation sum losses: 0.00h
19:43 madminer.utils.ml.tr INFO early stopping: 0.00h
19:43 madminer.utils.ml.tr INFO report epoch: 0.00h
19:43 madminer.ml INFO Saving model to models/sally
3. Evaluate score estimator#
Let’s evaluate the SM score on the test data
estimator.load('models/sally')
t_hat = estimator.evaluate_score(
x='data/samples/x_test.npy'
)
19:43 madminer.ml INFO Loading model from models/sally
19:43 madminer.utils.vario INFO Loading data/samples/x_test.npy into RAM
19:43 madminer.ml INFO Starting score evaluation
Let’s have a look at the estimated score and how it is related to the observables:
x = np.load('data/samples/x_test.npy')
fig = plt.figure(figsize=(10,4))
for i in range(2):
ax = plt.subplot(1,2,i+1)
sc = plt.scatter(x[:,0], x[:,1], c=t_hat[:,i], s=25., cmap='viridis', vmin=-1., vmax=1.)
cbar = plt.colorbar(sc)
cbar.set_label(r'$\hat{t}_' + str(i) + r'(x | \theta_{ref})$')
plt.xlabel(r'$p_{T,j1}$ [GeV]')
plt.ylabel(r'$\Delta \phi_{jj}$')
plt.xlim(10.,300.)
plt.ylim(-3.15,3.15)
plt.tight_layout()
plt.show()